The Schur Complement Method: Part 2
We continue our informal study of domain decomposition methods (DDMs).
We will describe non-overlaping DDMs in terms of differential operators as opposed to basic linear algebra operations. This will later allow us to easily describe more sophisticated parallel algorithms such as the Dirichlet-Neuman and Neuman-Neuman algorithms.
In order to go one step further in that study it is necessary to introduce some PDE related theory and lingo. However I will try to keep it light and will just introduce what is necessary to build an intuition.
2D Poisson approximation as the Frankenstein monster
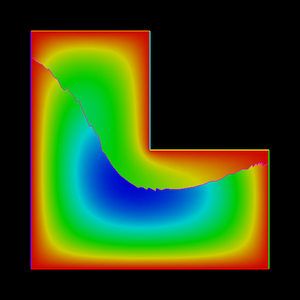
Last time we crafted an approximation, using the finite element method, of a function \(\varphi\) solution of the boundary problem
Refer to the first post regarding the choice of \(\Omega\) and the finite element space.
After delegating the assembly of the stiffness matrix and the load vector to the FreeFem++ software, we implemented the Schur complement method as a combination of unknown reordering and block Gaussian elimination applied to a global linear system.
In this part, I will describe how we can take into account the domain decompostion from the very begining, that is, in the formulation of the boundary problem itself.
Creating a monster
Let \(\Omega_{1}\) and \(\Omega_{2}\) the two non-overlaping subdomains introduced in the previous post and let \(\Gamma := \partial\Omega_{1} \cap \partial\Omega_{2}\), the boundary between \(\Omega_{1}\) and \(\Omega_{2}\).
Let \(\varphi_{1}\) (respectively \(\varphi_{2}\)) a (local) solution of \(\eqref{eq:globalPDE}\) restricted to \(\Omega_{1}\) (respectively \(\Omega_{2}\)):
Question
Is solving \(\eqref{eq:subdomainsPDE}\) solving \(\eqref{eq:globalPDE}\) ?
The answer is no. Here are a couple of examples to give you an intuition of what could go wrong:
Conclusion
Clearly, we need to pay more attention to what’s going on around \(\Gamma\).
Trace, flux and transmission conditions
So for now, our stuff looks like this

We need to add extra conditions to \(\eqref{eq:subdomainsPDE}\) in order to make the global solution more regular and eventualy satisfy \(\eqref{eq:globalPDE}\).
Trace
At the very least, the traces of the local solutions \(\varphi_{1}\) and \(\varphi_{2}\) on \(\Gamma\) should be equal in order to make the global solution continous:
Flux
Then we must ensure that the global solution is regular enough around the interface, that is, differentiable on \(\Gamma\).
In order to do so we will consider the normal derivatives along \(\Gamma\) of the local solutions \(\varphi_{1}\) and \(\varphi_{2}\), also know as flux, and balance them as illustrated in the following sketch:
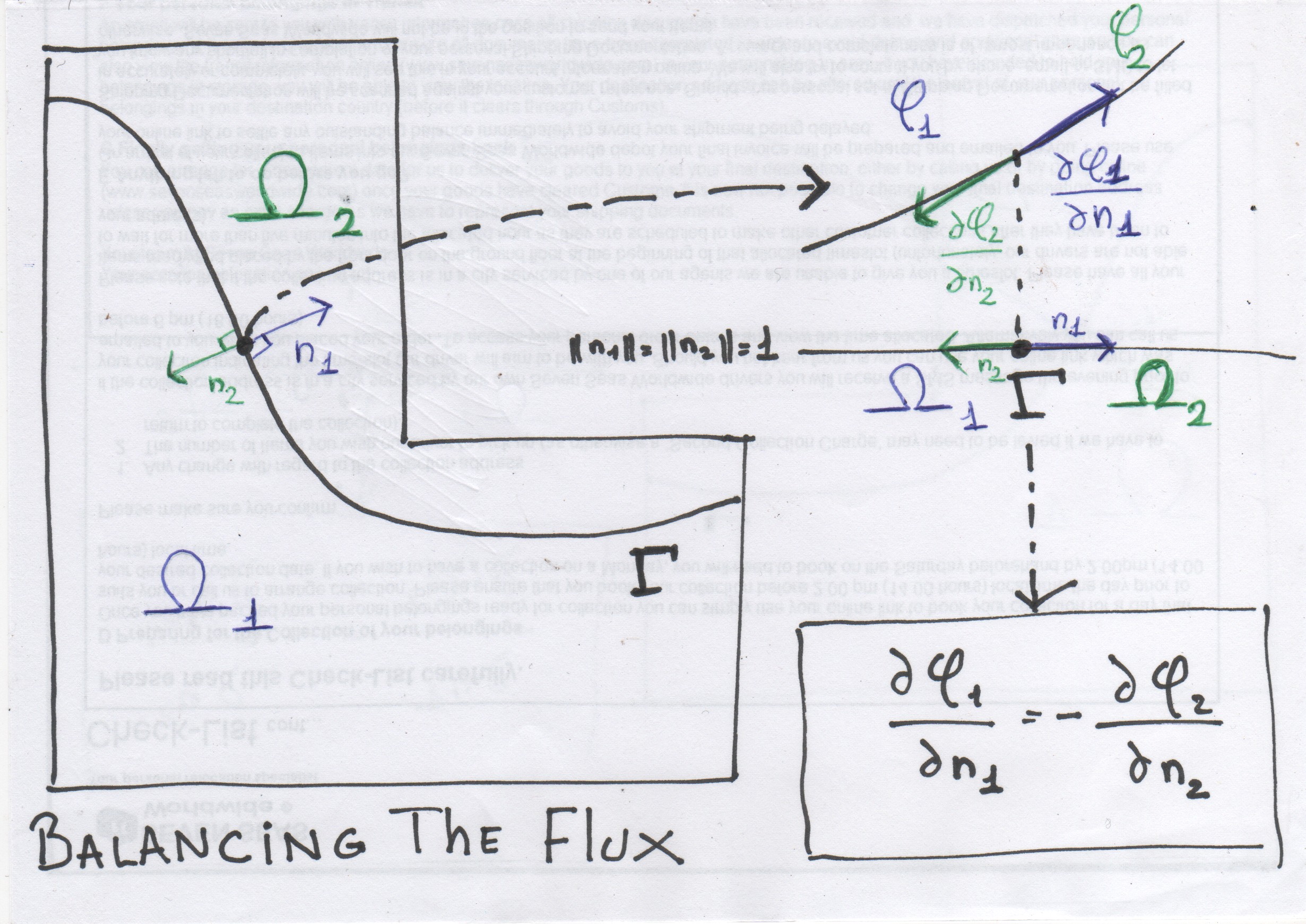
This can be concisely written as:
Just remember that the directions of \(n_{1}\) and \(n_{2}\) depend on the point of \(\Gamma\) under consideration.
\(\eqref{eq:transmissionOfTrace}\) and \(\eqref{eq:transmissionOfFlux}\) are known as the transmission conditions.
Putting everything together we end up with a new boundary problem:
Question
Is solving \(\eqref{eq:subdomainsPDEWithTransmition}\) solving \(\eqref{eq:globalPDE}\) ?
This time, under certain assumptions regarding \(\Gamma\), the answer is yes but we’re not going to talk about that here.
Conclusion
We crafted a problem taking into account a 2 domains decomposition by introducing the transmission conditions: one condition related to the trace on \(\Gamma\),
another condition related to the flux going through \(\Gamma\). Now, we’re left with a choice: either solve first for the trace or for the flux. But, before looking into that I would like to take the time to describe the main steps to translate this problem into linear algebra.
FEM for dummies
In this part I will try to explain as concisely as possible how to apply the FEM to \(\eqref{eq:globalPDE}\). But please keep in mind that it is oversimplified.
Weak formulation and discretization
So far, we never discussed which functional space the solution of \(\eqref{eq:globalPDE}\) should be chosen from.
So let \(H\) a finite-dimensional vector space of functions defined on \(\Omega\) vanishing on \(\partial\Omega\).
Let \(N:=dim(H)\) and \((e_{i})_{1 \leq i \leq N}\) a basis of \(H\).
I don’t want to discuss the gory functional analysis details here so just consider that I chose \(H\) so that everything I’m about to write works just fine.
We will search \(\varphi\) in \(H\).
In order to do so, we are going to design a “test” that \(\varphi\) must pass in order to be a solution of \(\eqref{eq:globalPDE}\).
In order to design that test we choose a function \(\psi\) in \(H\).
\(\psi\) is called a test function and we say that \(\varphi\) is tested against \(\psi\).
These are the key steps:
Weak formulation
- Start with what must be satisfied:
- Multiply by a test function
\(\psi\): -
Sum over the domain of definition:
-
Apply the Green-Ostrogradsky theorem (which is a generalisation of the integration by parts we were taught back in highschool) to the sinistral side of the equation. Since
\(\psi\)vanishes along\(\partial\Omega\), the line integral over\(\partial\Omega\)vanishes too (we take into account the boundary conditions): -
Let
\(a: (\psi,\varphi) \mapsto \int_\Omega \nabla\psi\nabla\varphi dxdy\)and\(b: \psi \mapsto -\int_\Omega \psi dxdy\). It is important to remark that\(a\)(respectively\(b\)) is a bilinear (respectively linear) form. We can concisely re-write the previous equation:
Discretization
-
Since we chose
\(\psi\)in a finite-dimensional vector space, and since\(a\)and\(b\)are linear with respect to\(\psi\). Instead of checking that the previous equation holds for any\(\psi\), we just need to check that it holds for each basis vector\((e_{i})_{1 \leq i \leq N}\): -
Again, since we chose
\(\varphi\)in a finite-dimensional vector space, we can uniquely decompose\(\varphi\)as a linear combination with respect to the basis\((e_{i})_{1 \leq i \leq N}\):\(\varphi\ = \sum\limits_{i=1}^{N} \varphi_{i} e_{i}\). Since\(a\)is linear with respect to\(\varphi\), it comes: -
Let
\(A = (a(e_{i}, e_{j}))_{1 \leq i,j \leq N}\),\(x = (\varphi_{i})_{1 \leq i \leq N}\)and\(b = (b(e_{j}))_{1 \leq j \leq N}\). We can rewrite the previous equation as a product between a matrix and a vector :
So here we are, we started looking for \(\varphi \in H\) and we end up looking for \(x \in \mathbf{R}^{N}\). All we have to do now is to compute \(A\) and \(b\), and then solve for \(x\) (note that we could just compute the effect of multiplying a vector by \(A\) if we were to use an iterative solver as explained in the previous post).
Computation of the discrete operators
The next step is to compute
and
but in order to do so, we must describe what are \(H\) and \((e_{i})_{1 \leq i \leq N}\).
So let \(H\) be the space of continuous piecewise linear functions over the triangulation of \(\Omega\) (introduced in the previous post) and vanishing on \(\partial \Omega\). The dimension of \(H\), \(N\), is equal to the number of vertices in the interior of \(\Omega\).
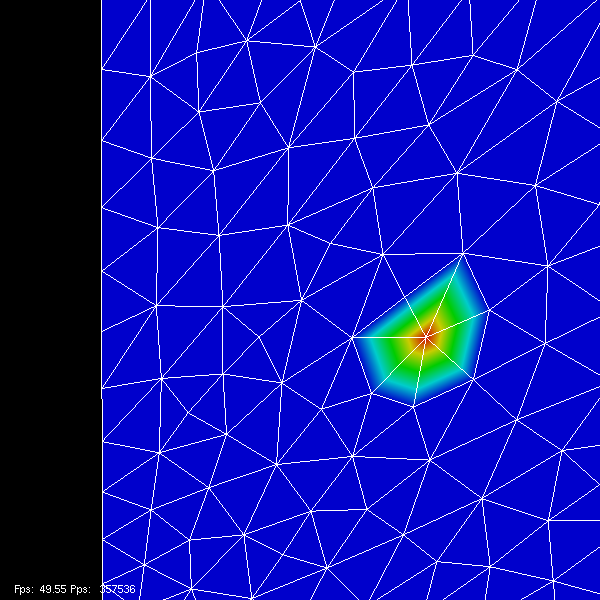
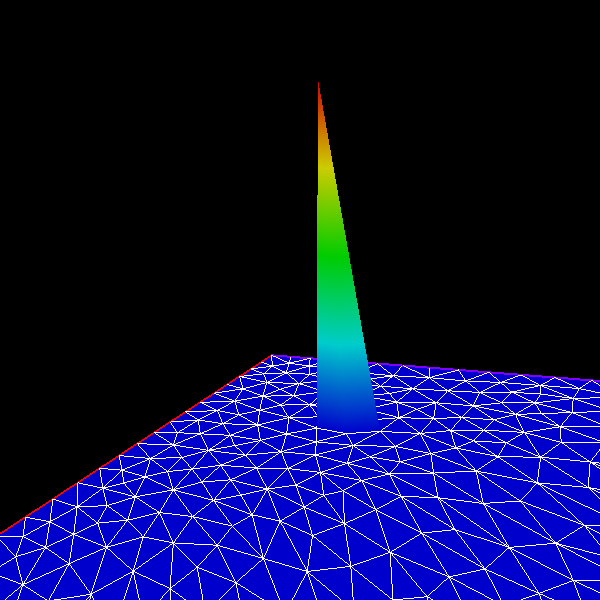
Introducing the tent functions
So what is a basis of \(H\) ?
Let \((q_{i})_{1 \leq i \leq N}\) the vertices of the triangulation.
Then, let’s choose \((e_{i})_{1 \leq i \leq N}\) to be the tent functions defined as follow:
and here is what a tent function looks like:
Any function in \(H\) can be uniquely decompossed as a linear combination of tent functions.
We got everything we need to compute \(A_{i,j}\) and \(b_{i}\).
We just need to walk the triangles.
Computing \(b\)
Let’s start with the easy one. Given a triangle \(T_{i} = (q_{i_{1}},q_{i_{2}},q_{i_{3}})\) what are the contributions to \(b\) ?
We got 3 contributions: one to \(b_{i_{1}}\) from \(e_{i_{1}}\), one to \(b_{i_{2}}\) from \(e_{i_{2}}\) and one to \(b_{i_{3}}\) from \(e_{i_{3}}\).
And the contributions are equal to:
Now using this handy quadrature formula which is exact for affine function:
where \(|T_{i}|\) is the area of \(T_{i}\),
If \(k^- = 1 + ((k -2) \mod 3)\) and \(k^+ = 1 + (k \mod 3)\), we end up with:
Done ! Next !
Computing \(A\)
First of all, let’s remark that when \(q_{i}\) and \(q_{j}\) never belong to a same triangle then the supports of \(e_{i}\) and \(e_{j}\) are disjoint and therefore \(A_{i,j}\) is zero.
Otherwise, given a triangle \(T_{i} = (q_{i_{1}},q_{i_{2}},q_{i_{3}})\), \(e_{i_{1}}\restriction_{T_{i}}\), \(e_{i_{2}}\restriction_{T_{i}}\) and \(e_{i_{3}}\restriction_{T_{i}}\) being affine, their gradiants, \(\nabla e_{i_{1}}\restriction_{T_{i}}\), \(\nabla e_{i_{2}}\restriction_{T_{i}}\) and \(\nabla e_{i_{3}}\restriction_{T_{i}}\) are constants. Therefore:
So we’re left with computing \(\nabla e_{i_{j}}\restriction_{T_{i}}, 1 \leq j \leq 3\).
We will do that geometricaly on a sketch:
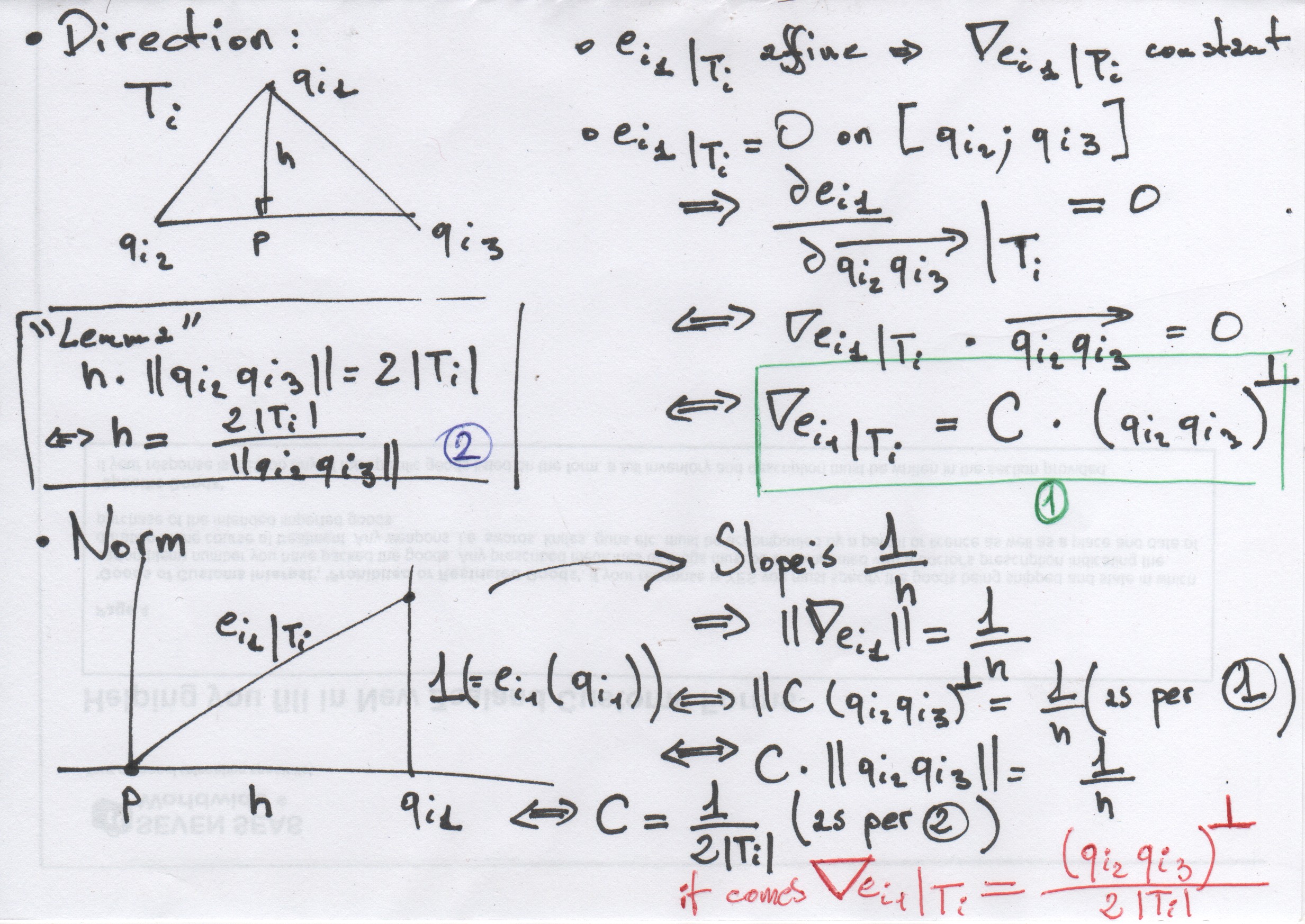
We end up with:
which is easy to compute.
Implementation
We got everything now. Here is a baby implementation of the method in Javascript/WebGL.
Sub-assembling
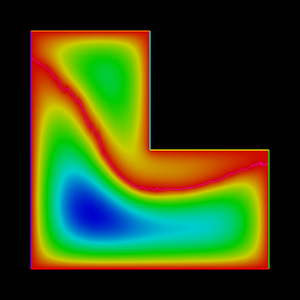
If we apply the same procedure, restricted to each subdomain and if we use the same unknown reordering techniques introduced in the previous post, we can assemble two linear (sub-)systems:
where
\(A^{(i)}_{II}\)is the block coupling the interior of domain\(i\)to itself;\(A^{(i)}_{\Gamma\Gamma}\)is the block coupling the interface to itself BUT only considering the triangles of domain\(i\);\(A^{(i)}_{\Gamma I}\)is the block coupling the interface to the interior of domain\(i\);\(A^{(i)}_{I\Gamma}\)is the block coupling the interior of domain\(i\)to the interface
Now, given these two linear systems, we can try to write a discrete analog of \(\eqref{eq:subdomainsPDEWithTransmition}\).
A discrete analog of \(\eqref{eq:subdomainsPDE}\) is:
But we know that is not enough, we need to take care of the transmission conditions as well.
Discrete transmition conditions
Trace
Transmission of the trace, \(\eqref{eq:transmissionOfTrace}\), is simply written as:
Flux
Transmission of the flux, \(\eqref{eq:transmissionOfFlux}\), is trickier.
How do we evaluate \(\frac{\partial\varphi_i}{\partial n_i}, i=1,2\) ?
In order to do so we have to step back a little bit and re-write \(\eqref{eq:weakFormulation}\) for a subdomain:
So what we have is an expression of \( \psi \mapsto \oint_{\Gamma } \frac{\partial \varphi_i}{\partial n_i}\psi d\sigma \) the dual of \(\frac{\partial\varphi_i}{\partial n_i}\) in the weak topology of \(H_i\). Since I said we will skip all the functional analysis details,
just consider that “the flux transmission condition works the same in the weak topology”.
Particularizing \(\eqref{eq:weakNeuman}\) only for \( \psi = e_{j}\) with \(q_{j}\) along \(\Gamma\) (otherwise the line integral is zero), a discrete analog of the “weak” flux is:
and then the discrete analog of the “weak” flux trasmition condition is:
Putting everything together we end up with the discrete analog of \(\eqref{eq:subdomainsPDEWithTransmition}\):
Conclusion
In that part I briefly described how to apply the FEM and to express discrete analog of the transmission conditions.
In the next one, we will show how solving \(\eqref{eq:discreteSubdomainsPDEWithTransmition}\) for the trace first is equivalent to what
was done in the previous post.
Trace first
Remember what we did last time after massaging the global linear system ?
We first solved
where \(\Sigma = A_{\Gamma\Gamma} - A^{(1)}_{\Gamma I}(A^{(1)}_{II})^{-1}A^{(1)}_{I\Gamma} - A^{(2)}_{\Gamma I}(A^{(2)}_{II})^{-1}A^{(2)}_{I\Gamma}\)
and \(\tilde{b} = b_{\Gamma} - A^{(1)}_{\Gamma I}(A^{(1)}_{II})^{-1}b^{(1)}_{I} - A^{(2)}_{\Gamma I}(A^{(2)}_{II})^{-1}b^{(2)}_{I}\)
and then solved
Let’s see why it’s equivalent to solve \(\eqref{eq:discreteSubdomainsPDEWithTransmition}\) for the trace first.
Previous post revisited
The idea is to craft a “trace only” equation.
-
From the first equation in
\(\eqref{eq:discreteSubdomainsPDEWithTransmition}\)comes -
Injecting that expression of
\(x^{(i)}_{I}\)in the flux transmission equation (the third equation in\(\eqref{eq:discreteSubdomainsPDEWithTransmition}\)) leads to -
Because of the trace transmission equation (the second equation in
\(\eqref{eq:discreteSubdomainsPDEWithTransmition}\)) this is equivalent to
That’s it ! Same !
Implementation & Conclusion
See the previous post for the details :-)
Flux first
Neumann problem
This time we need to craft a “flux only” equation.
-
Assemble two linear systems from
\(\eqref{eq:weakNeuman}\), that is, taking into account the flux, as a Neumann boundary condition: -
Perform the same block Gaussian elimination we did in the previous post, in order to find an expression of
\(x^{(i)}_{\Gamma}\):concisely written as
where
\(\Sigma^{(i)} := A^{(i)}_{\Gamma\Gamma} - A^{(i)}_{\Gamma I}(A^{(i)}_{II})^{-1}A^{(i)}_{I\Gamma}\)and\(\tilde{b}^{(i)} := b^{(i)}_{\Gamma} - A^{(i)}_{\Gamma I}(A^{(i)}_{II})^{-1}b^{(i)}_{I}\) -
Inject into the trace transmission condition equation:
-
Apply the flux transmission condition:
concisely written as
where
\(\tilde{\Sigma} := (\Sigma^{(1)})^{-1} + (\Sigma^{(2)})^{-1}\)and\(\tilde{\tilde{b}} := (\Sigma^{(2)})^{-1} \tilde{b}^{(2)} - (\Sigma^{(1)})^{-1}\tilde{b}^{(1)}\)
That’s it ! Here is the “flux only” equation. All we have to do now is solve for \(\lambda\), inject in \(\eqref{eq:discreteNeumann}\) and solve for each subdomain.
Implementation
Here is my implementation of the “flux first” method with sub-assembling:
1 function schurComplementMethod2()
2
3 [vertices, triangles, border, domains] = readMesh("poisson2D.mesh");
4 interface = readInterface("interface2.vids");
5
6 % Assemble local Dirichlet problems
7 % => could be done in parallel
8 [A1, b1, vids1] = subAssemble(vertices, triangles, border, domains, interface, 1);
9 [A2, b2, vids2] = subAssemble(vertices, triangles, border, domains, interface, 2);
10
11 nbInterior1 = length(b1) - length(interface);
12 nbInterior2 = length(b2) - length(interface);
13
14 % LU-factorize the interior of the subdomains, we're going to reuse this everywhere
15 % => could be done in parallel
16 [L1, U1, p1, tmp] = lu(A1(1:nbInterior1, 1:nbInterior1), 'vector');
17 q1(tmp) = 1:length(tmp);
18 [L2, U2, p2, tmp] = lu(A2(1:nbInterior2, 1:nbInterior2), 'vector');
19 q2(tmp) = 1:length(tmp);
20
21 % In order to solve for the flux first, we need to compute the corresponding second member
22 % => could be done in parallel
23 bt1 = computeBTildI(A1, b1, nbInterior1, L1, U1, p1, q1);
24 bt2 = computeBTildI(A2, b2, nbInterior2, L2, U2, p2, q2);
25
26 epsilon = 1.e-30;
27 maxIter = 600
28
29 % Each pcg contributing to the second member could be done in parallel
30 btt = pcg(@(x) multiplyByLocalSchurComplement(A2, nbInterior2, L2, U2, p2, q2, x), ...
31 bt2, epsilon, maxIter) ...
32 - pcg(@(x) multiplyByLocalSchurComplement(A1, nbInterior1, L1, U1, p1, q1, x), ...
33 bt1, epsilon, maxIter);
34
35 % Solve for the flux => each nested pcg contribution could be done in parallel
36 flux = pcg(@(x) pcg(@(y) multiplyByLocalSchurComplement(A1, nbInterior1, L1, U1, p1, q1, y), ...
37 x, epsilon, maxIter) ...
38 + pcg(@(y) multiplyByLocalSchurComplement(A2, nbInterior2, L2, U2, p2, q2, y), ...
39 x, epsilon, maxIter), btt, epsilon, maxIter);
40
41 % Add the computed Neumann data to the load vectors
42 b1(nbInterior1 + 1 : end) += flux;
43 b2(nbInterior2 + 1 : end) -= flux;
44 % and solve the corresponding problems using a direct method
45 % => could be done in parallel
46 solution = zeros(length(vertices), 1);
47 solution(vids1) = A1 \ b1;
48 solution(vids2) = A2 \ b2;
49
50 writeSolution("poisson2D.sol", solution);
51
52 endfunction
53
54 function [A, b, dVertexIds] = subAssemble(vertices, triangles, border, domains, interface, domainIdx)
55 % Keep the triangles belonging to the subdomain
56 dTriangles = triangles(find(domains == domainIdx),:);
57 dVertexIds = unique(dTriangles(:));
58
59 % Put the interface unknowns at the end, using the numbering we computed in the last post
60 dVertexIds = [setdiff(dVertexIds, interface); interface];
61
62 % Switch domain triangles to local vertices numbering
63 % Should use a hashtable here but their is none in octave ...
64 globalToLocal = zeros(length(vertices), 1);
65 globalToLocal(dVertexIds) = 1:length(dVertexIds);
66 dTriangles(:) = globalToLocal(dTriangles(:));
67
68 % Assemble the Dirichlet problem
69 [A, b] = assemble(vertices(dVertexIds, :), dTriangles, border(dVertexIds));
70 endfunction
71
72 function [A, b] = assemble(vertices, triangles, border)
73 nvertices = length(vertices);
74 ntriangles = length(triangles);
75
76 iis = [];
77 jjs = [];
78 vs = [];
79
80 b = zeros(nvertices, 1);
81 for tid=1:ntriangles
82 q = zeros(3,2);
83 q(1,:) = vertices(triangles(tid, 1), :) - vertices(triangles(tid, 2), :);
84 q(2,:) = vertices(triangles(tid, 2), :) - vertices(triangles(tid, 3), :);
85 q(3,:) = vertices(triangles(tid, 3), :) - vertices(triangles(tid, 1), :);
86 area = 0.5 * det(q([1,2], :));
87 for i=1:3
88 ii = triangles(tid,i);
89 if !border(ii)
90 for j=1:3
91 jj = triangles(tid,j);
92 if !border(jj)
93 hi = q(mod(i, 3) + 1, :);
94 hj = q(mod(j, 3) + 1, :);
95
96 v = (hi * hj') / (4 * area);
97
98 iis = [iis ii];
99 jjs = [jjs jj];
100 vs = [vs v];
101 end
102 end
103 b(ii) += -area / 3;
104 end
105 end
106 end
107 A = sparse(iis, jjs, vs, nvertices, nvertices, "sum");
108 endfunction
109
110 function [bti] = computeBTildI(A, b, nbInterior, L, U, p, q)
111 bti = b(nbInterior + 1 : end) ...
112 - A(nbInterior + 1 : end, 1:nbInterior) * (U \ (L \ b(1:nbInterior)(p)))(q);
113 endfunction
114
115 function [res] = multiplyByLocalSchurComplement(A, nbInterior, L, U, p, q, x)
116 res = A(nbInterior + 1 : end, nbInterior + 1 : end) * x ...
117 - A(nbInterior + 1 : end, 1:nbInterior) * (U \ (L \ (A(1:nbInterior, nbInterior + 1 : end) * x)(p)))(q);
118 endfunction
119
120 function [vertices, triangles, border, domains] = readMesh(fileName)
121
122 fid = fopen (fileName, "r");
123
124 % Vertices
125 fgoto(fid, "Vertices");
126
127 [nvertices] = fscanf(fid, "%d", "C");
128 vertices = zeros(nvertices, 2);
129 for vid=1:nvertices
130 [vertices(vid, 1), vertices(vid, 2)] = fscanf(fid, "%f %f %d\n", "C");
131 end
132
133 % Edges
134 border = zeros(nvertices, 1);
135 fgoto(fid, "Edges");
136 [nedges] = fscanf(fid, "%d", "C");
137 for eid=1:nedges
138 [v1, v2] = fscanf(fid, "%d %d %d\n", "C");
139 border(v1) = 1;
140 border(v2) = 1;
141 end
142
143 % Elements
144 fgoto(fid, "Triangles");
145 [ntriangles] = fscanf(fid, "%d", "C");
146 triangles = zeros(ntriangles, 3);
147 domains = zeros(ntriangles, 1);
148 for tid=1:ntriangles
149 [triangles(tid, 1), triangles(tid, 2), triangles(tid, 3), domains(tid)] = fscanf(fid, "%d %d %d %d\n", "C");
150 end
151
152 fclose(fid);
153 endfunction
154
155 function [interface] = readInterface(fileName)
156 fid = fopen (fileName, "r");
157 interface = [];
158 while (l = fgetl(fid)) != -1
159 [vid] = sscanf(l, "%d\n", "C");
160 interface = [interface; vid];
161 end
162 fclose(fid);
163 end
164
165 function [] = fgoto(fid, tag)
166 while !strcmp(fgetl(fid),tag)
167 end
168 endfunction
169
170 function [] = writeSolution(fileName, solution)
171 fid = fopen (fileName, "w");
172 fprintf(fid, "MeshVersionFormatted 1\n\nDimension 2\n\nSolAtVertices\n%d\n1 1\n\n", length(solution));
173 for i=1:length(solution)
174 fprintf(fid, "%e\n", solution(i));
175 end
176 fclose(fid);
177 endfunctionConclusion
Solving for the flux first is a bit more involved and less efficient since we have to deal with the inverse of the local Schur complement. I believe that in practice this method is never used. Nevertheless introducing the flux and the Neumann problems is a necessary step to understand the Dirichlet-Neuman and Neuman-Neuman algorithms. Someday I will try to post about that, but it will be later.
Conclusion
The next time, I would like to experiment with something more ambitious: I will try to solve the mild-slope equation in the Lyttelton port using more than two domains decompostion (trace first). I will try to use fancy stuff like MPI and GPU linear algebra libraries. Stay tuned !
blog comments powered by Disqus